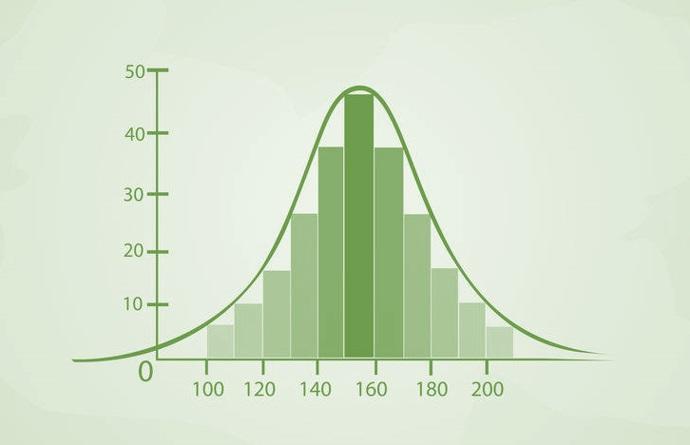
📊 数据分析直方图:数据可视化的经典工具
🌟 直方图的基本概念
直方图是数据分析中最基础也最强大的可视化工具之一!✨ 它通过将连续数据分成若干个区间(称为"bin"或"箱"),然后统计每个区间内数据点的数量,最后以柱状图的形式展示出来。📊
直方图的特点:
- 直观展示数据分布形态 🌀
- 揭示数据集中趋势和离散程度 📈
- 帮助识别异常值和数据模式 🔍
- 适用于大样本量的数据分析 💯
🔍 直方图与条形图的区别
很多小伙伴容易混淆直方图和条形图,其实它们有本质区别哦!🤓
| 特征 | 直方图 | 条形图 |
|---|---|---|
| 数据类型 | 连续数据 | 分类数据 |
| 柱子间距 | 通常无间距 | 有明显间距 |
| X轴含义 | 数值范围区间 | 具体类别 |
| 排序方式 | 按数值大小 | 可任意排序 |
💡 直方图的五大应用场景
- 质量检测 👩🔬:检查产品尺寸、重量等是否符合标准分布
- 金融分析 💰:分析股票收益率、交易量等分布情况
- 用户行为研究 📱:统计用户停留时长、点击次数等
- 医学研究 🏥:分析患者年龄、血压值等生理指标
- 教育评估 📚:查看考试成绩分布,识别教学问题
🛠️ 创建优质直方图的技巧
想要制作出专业又美观的直方图?这些小技巧快收好!🎯
选择合适的分箱数量:
- 太多箱子 → 图形过于分散杂乱 😵
- 太少箱子 → 掩盖重要细节 🧐
- 经验法则:√n(n为数据点数)或Sturges公式
美化技巧:
- 使用渐变色填充柱子 🌈
- 添加数据标签和参考线 📝
- 保持适当的宽高比例 📏
- 添加有意义的标题和轴标签 ✏️
📈 直方图进阶分析
数据分析高手还会通过这些方法从直方图中提取更深层信息!🧠
偏态分析:
- 右偏(正偏):平均值>中位数>众数 ↗️
- 左偏(负偏):平均值<中位数<众数 ↖️
- 对称分布:三者重合 ⏸️
峰度分析:
- 高峰度:数据集中在均值附近 🏔️
- 低峰度:数据分布较平坦 🏖️
- 正常峰度:类似正态分布 ⛰️
🌐 网友热评
- @数据小达人:"直方图真是数据分析的瑞士军刀!每次做报告老板都夸我图表专业~ 💼✨ #数据分析必备"
- @统计小白:"原来直方图有这么多门道!以前只知道画柱子,现在学会看偏态和峰度了,感谢分享!📚🙏 #学习成长"
- @可视化设计师:"配色和分箱技巧太实用了!客户说我的图表既美观又专业,业绩提升30%!🎨💯 #设计价值"
- @AI研究员:"在机器学习特征工程中,直方图帮我们快速理解数据分布,是EDA不可或缺的工具!🤖🔬 #AI实战"
- @商业分析师:"用直方图分析销售数据后,发现了隐藏的客户群体,直接促成新产品线开发!📊🚀 #商业洞察"
百科知识